栈和队列
栈
定义
- 只允许在一端进行插入或删除操作的线性表
- 逻辑结构:与普通线性表相同
- 运算:插入、删除操作有区别
- 栈顶:允许插入和删除的一端,对应元素被称为栈顶元素
- 栈底:不允许插入和删除的一端,对应元素被称为栈底元素
- 特点:后进先出(LIFO)
基本操作
InitStack(&S)初始化。构造一个空栈,分配内存空间DestroyStack(&S)销毁。销毁并释放栈S所占用的内存空间Push(&S, x)进栈。若栈S未满,则将x加入并称为新栈顶Pop(&S, &x)出栈。若栈S非空,则弹出栈顶元素,并用x返回GetTop(S, &x)读栈顶元素。若栈S非空,则用x返回栈顶元素Empty(S)判断一个栈是否为空
n个不同元素进栈,出栈元素不同排列的个数为 $\frac{1}{n+1}C_{2n}^{n}$
顺序存储结构
栈的定义和初始化

进栈操作

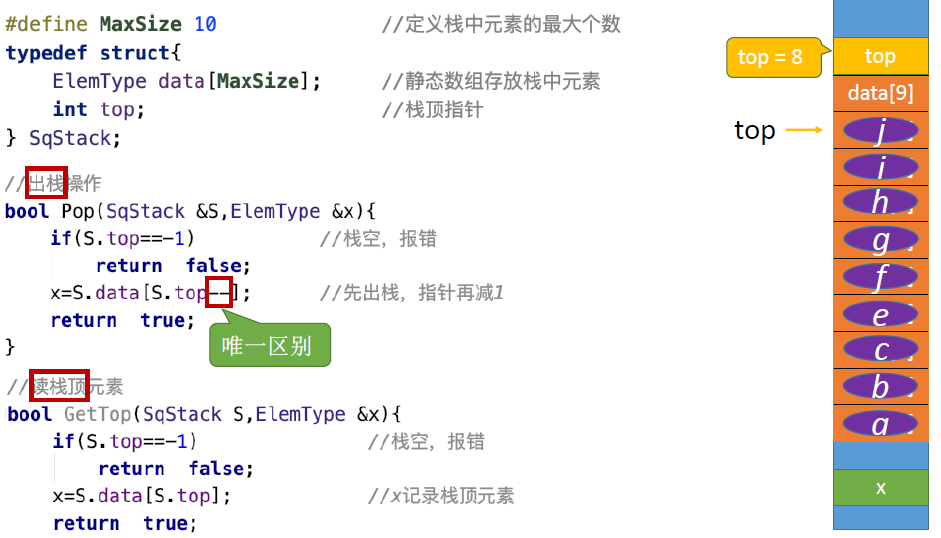
出栈操作

读取栈顶元素
共享栈
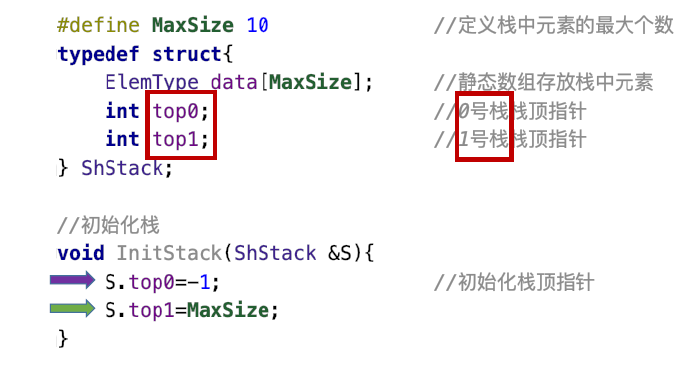
- 使用静态数组要求提前分配空间,造成资源浪费,所以共享栈应运而生
- 两个栈共享同一片空间,0,1号栈朝同一方向进栈
- 栈满的条件: top0 + 1 = top1
链式存储结构
- 进栈:头插法建立单链表,对头节点的后插操作
- 出栈:单链表的删除操作,对头节点的删除操作
- 推荐使用不带头节点的链表
- 创建、销毁、增、删、查的操作参考链表
定义

队列
定义
- 只允许在一端进行插入,在另一端删除的线性表
- 队头:允许删除的一端,对应的元素称为队头元素
- 队尾:允许插入的一端,对应的元素成为队尾元素
- 特点:先进先出(FIFO)
基本操作
InitQueue(&Q)初始化。构造一个空队列DestroyQueue(&Q)销毁队列。销毁并释放队列Q所占用的内存空间EnQueue(&Q, x)入队列。若队列Q未满,将x加入,成为新队尾DeQueue(&Q, &x)出队列。若队列非空,删除队头,并用x返回GetHead(Q, &x)读队头元素。若队列非空,将队头元素赋值给xQueueEmpty(Q)队列判空
顺序存储结构
初始化

入队
- 通过取余操作,只要队列不满,就可以一直用之前已经出队列的空间,逻辑上实现了循环队列的操作
- 队列已满的条件:队尾指针的再下一个位置是队头,即
(Q.rear + 1) % MaxSize == Q.front - 代价:牺牲了一个存储单元,因为如果rear和front相同,与判空条件相同了

出队
实际上获取队头元素的值就是出队操作去掉队头指针后移的代码
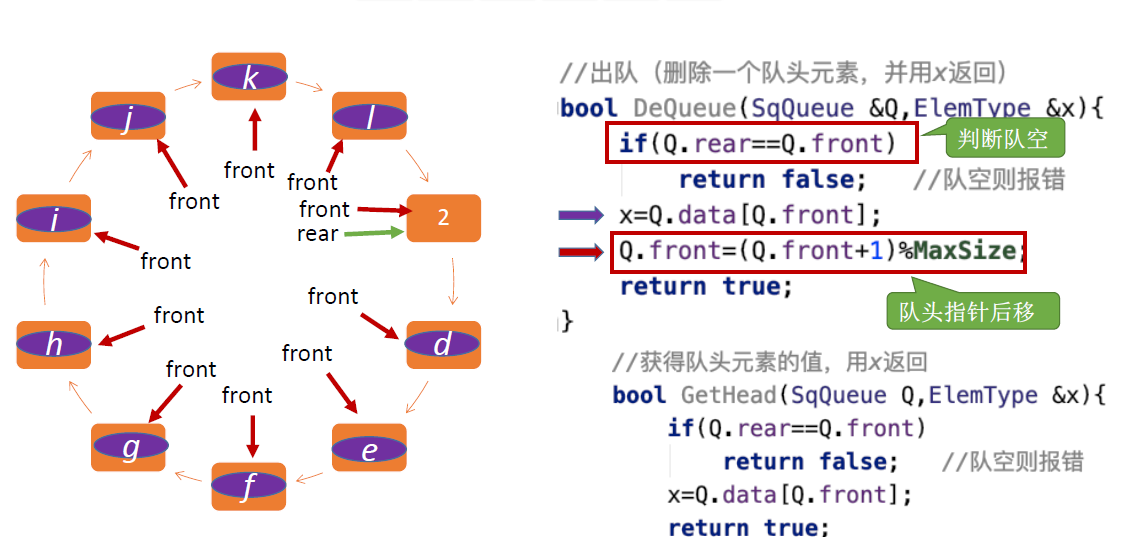
判空
方案1
- 使用前面讲的牺牲一个存储空间方式来解决
- 初始化时,rear=front=0
- 队列元素个数:(rear + MaxSize - front) % MaxSize
- 队列已满的条件:队尾指针的再下一个位置是队头,即(Q.rear + 1) % MaxSize == Q.front
- 判空条件:Q.rear == Q.front
方案2
- 不牺牲一个存储空间,在结构体内多建立一个变量size
- 初始化时,rear = front = 0; size = 0;
- 队列元素个数: size
- 插入成功: size++;删除成功:size–
- 队满条件:size == MaxSize
- 判空条件:size == 0
方案3
- 不牺牲一个存储空间,在结构体中多建立一个变量tag
- 初始化时,rear = front = 0; tag = 0
- 因为只有删除操作才有可能为空,只有插入操作才有可能满
- 每次删除成功时,都让tag = 0
- 每次插入操作时,都让tag = 1
- 队满条件:front == rear && tag == 1
- 队空条件:front == rear && tag == 0
- 元素个数:(rear + MaxSize - front) % MaxSize
链式存储结构
初始化-带头节点

初始化-不带头节点

入队-带头节点

入队-不带头节点

出队-带头节点
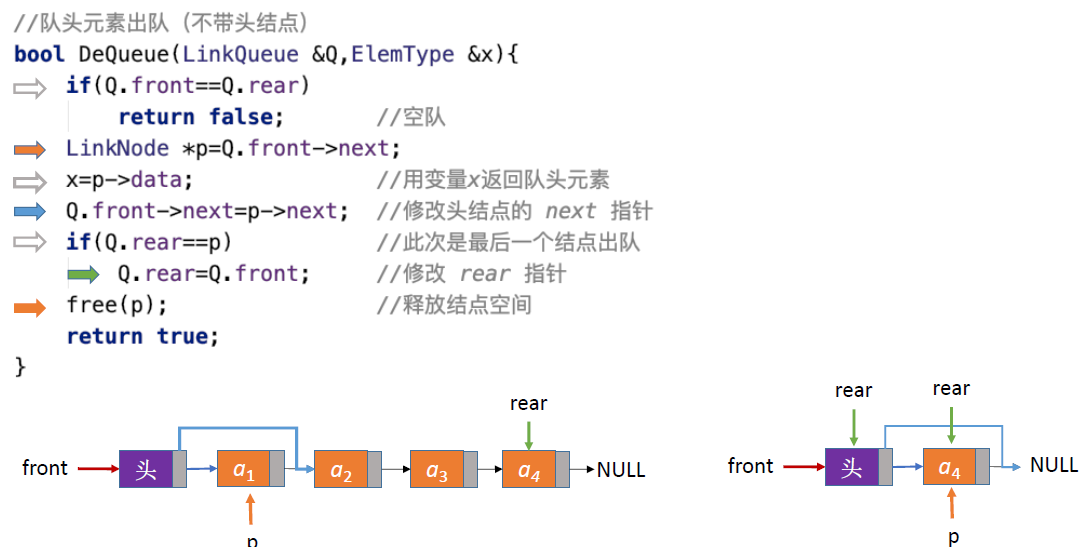
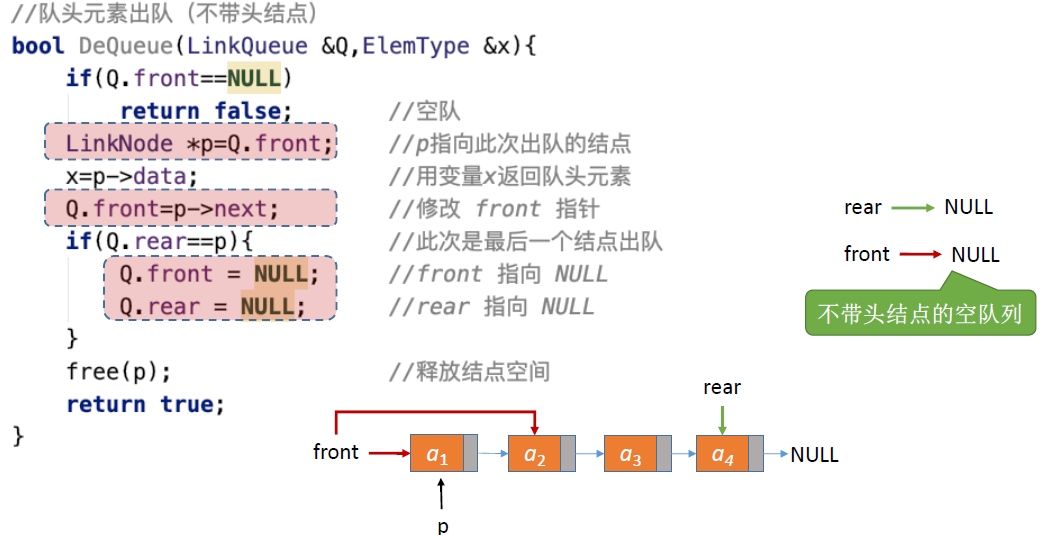
出队-不带头节点
队满条件
- 顺序存储:预分配空间耗尽
- 链式存储:一般不会满,除非内存不足
- 因此不用考虑队满
双端队列
定义
- 双端队列:只允许两端插入,两端删除的线性表
- 输入受限的双端队列:只允许一端输入,两端都删除的线性表
- 输出受限的双端队列:只允许两端输入,一端删除的线性表
特点
- 在栈中合法的输出序列,在双端队列中必定合法
栈在括号匹配中的应用
- 若有括号无法匹配则出现编译错误
- 遇到左括号就入栈
- 遇到右括号就消耗一个左括号
实现

栈在求值表达式中的应用
- 由三个部分组成:操作数,运算符,界限符
- 平时写的表达式都是中缀表达式
- 逆波兰表达式=后缀表达式
- 波兰表达式=前缀表达式

中缀转后缀
- 确定中缀表达式各个运算符的顺序
- 选择下一个运算符,按照左操作数、右操作数、运算符的方式组合成一个新的操作数
- 如果还有运算符没有被处理,则进行第二步
- 左优先原则:只要左边的运算符能先计算,就优先计算左边的
实现
- 初始化一个栈,用于保存暂时还不能确定运算顺序的运算符,从左到右处理各个元素,可能遇到三种情况
- 遇到操作数,直接加入后缀表达式
- 遇到界限符,左括号-入栈,右括号-依次弹出栈内运算符并加入后缀表达式,直到遇到左括号
- 遇到运算符,依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,如果遇到左括号或空,则停止。之后再把当前运算符入栈
- 将栈中剩余运算符弹出加入后缀表达式
后缀表达式计算
- 从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数进行运算,合体为一个操作数
- 注意两个操作数的左右顺序
- 特点:最后出现的操作数有限被运算,LIFO,可以用栈完成
- 左优先原则:只要左边能计算,就先计算左边的
实现
- 从左扫描一下元素,直到完成所有元素
- 操作数:压入栈,并回到第一步,否则执行第三步
- 运算符:弹出两个栈顶元素,执行相应运算,结果返回栈顶,回到第一步
- 表达式合法,则会留下一个元素,就是最终结果
中缀转前缀
- 确定中缀表达式各个运算符的顺序
- 选择下一个运算符,按照运算符,左操作数,右操作数的方式组合成一个新的操作数
- 如果有运算符没有被处理,则进行第二步
- 右优先原则:只要右边能优先计算的,就先算右边的
前缀表达式计算
- 初始化两个栈,操作数栈和运算符栈
- 扫描到操作数,压入操作数栈
- 扫描到运算符或界限符,按照中缀转后缀相同的逻辑雅茹运算符栈(期间也会弹出运算符,每当弹出一个运算符,就需要弹出两个操作数栈的栈顶元素并执行相应的运算,运算结果再压入操作数栈
栈在递归中的应用
函数调用特点
- 最后被调用的函数最先执行结束
- 函数调用时,需要用一个栈存储信息(调用返回地址,实参,局部变量)
队列的应用
- 树的层次遍历
- 图的广度优先搜索
- 操作系统中的应用(进程调用-先来先服务,CPU资源分配,打印数据缓冲区)
特殊矩阵压缩存储
一维数组的存储结构
- 起始地址:LOC
- 各数组元素大小相同,且物理上连续存放
- 数组元素a[i]的存放地址=LOC + i * sizeof(ElemType)
二维数组的存储结构
- 分为行优先和列优先,本质就是把二维数组转为一维空间存储
- 按行优先,则b[i][j]的地址为LOC + (i * N + j) * sizeof(ElemType)
- 按列优先,则b[i][j]的地址为LOC + (i + M * j) * sizeof(ElemType)
对称矩阵压缩
- 策略:只存储主对角线+下三角区,按行优先原则将各个元素存入到一维数组中
- 大小:(n + 1) * n / 2
- ai,j是第几个元素?
三角矩阵压缩
- 策略:行优先原则,将三角区存入一维数组中,并在最后一个存入常量c
稀疏矩阵压缩
- 策略1:顺序存储,三元组(i-行,j-列,v-值)
- 策略2:链式存储,十字链表法